Температурные воздействия на конструкции – Часть 2: Термомеханика
В этой части рассмотрены теоретические основы температурных воздействий на конструкции с точки зрения классической механики материалов.
В предыдущей части 1 рассмотрены особенности учета температурных воздействий при проектировании конструкций зданий по российскому своду правил СП 20.13330.2011 (СНиП 2.01.07-85).
В части 3 представлены примеры температурных воздействий на простые конструкции – балки с различными условиями закрепления.
1. Теоретические основы температурных воздействий на материалы
1.1. Температурное расширение-сокращение
Изменения температуры вызывают расширение или сокращение конструкционных материалов, в результате чего в них возникают температурные деформации и температурные напряжения. Простая иллюстрация температурного расширения показана на рисунке 2.1, где брусок материала не закреплен и поэтому имеет возможность свободно расширяться [1].

Рисунок 2.1 – Брусок материала под воздействием увеличения температуры [1]
Когда этот брусок нагревается, каждый элемент материала подвергается температурным деформациям по всем направлениям, и, соответственно, размеры бруска увеличиваются также во всех направлениях. Если взять угол А за точку отсчета и дать стороне АВ возможность сохранять свое исходное направление, то брусок примет форму, которая показана штриховыми линиями.
Для большинства конструкционных материалов температурная деформация εT является пропорциональной изменению температуры ΔT, то есть
εT = α·ΔT, (1)
где α – свойство материала, которое называется коэффициентом температурного расширения. Согласно принятому в мире «знаковому соглашению» температурное расширение считается положительным, а температурное сокращение – отрицательным [1, 2].
1.2. Коэффициент температурного расширения конструкционных материалов
Поскольку деформация является безразмерной величиной, этот коэффициент температурного расширения имеет размерность, обратную изменению температуры. В системе СИ размерность αТ может выражаться как 1/К (величина обратная единице СИ Кельвин) или 1/ºС (величина обратная градусу Цельсия). Величина αТ является одинаковой в обоих случаях, так как изменение температуры является численно одинаковым как в градусах Кельвина, так и в градусах Цельсия.
Удобно представлять величину коэффициента температурного расширения в единицах 10 -6 /ºС или мкм/м·ºС. Последний вид особенно удобен – он наглядно показывает насколько микрометров удлиняется один метр материала при увеличении температуры на один градус температуры.
Информация о коэффициентах температурного расширения некоторых конструкционных материалов представлена в таблице 1.
Таблица 2.1 — Коэффициент температурного расширения конструкционных материалов [1]

1.3. Коэффициент температурного расширения алюминиевых сплавов
Коэффициенты температурного расширения основных алюминиевых сплавов, которые применяются в строительстве, показаны в таблице 2.
Таблица 2.2 — Коэффициент температурного расширения строительных алюминиевых сплавов [3]

Из таблицы 2.2 видно, что коэффициенты температурного расширения различных алюминиевых сплавов различаются незначительно. Поэтому в своде правил СП 128.13330.2012 (СНИП 2.03.06-85) для расчетов алюминиевых конструкций в интервале температуры от минус 70 ºС до 100 ºС для всех применяемых в строительстве алюминиевых сплавов применяется коэффициент температурного расширения 0,23·10 -4 1/ºС [4]. В европейском стандарте EN 1991-1-5 величина расчетного коэффициента температурного расширения составляет 24·10 -6 1/ºС [5].
1.4. Температурные напряжения
Чтобы продемонстрировать относительную важность температурных напряжений, можно сравнить температурные напряжения с напряжениями, которые возникают при силовом нагружении [1]. Предположим, что мы имеем брус, который нагружен силами в осевом направлении с продольными деформациями, которые даются равенством
где σ – напряжение, а Е – модуль упругости. Далее предположим, что мы имеем идентичный брусок, которые подвержен изменению температуры ΔT. Это означает, что этот брусок имеет температурные деформации согласно равенства (1). Приравнивание этих двух видов деформаций дает уравнение
σ = Е·α·ΔT (3)
Вычислим осевое напряжение σ, которое дает такие же деформации, как и изменение температуры ΔT в стержнях из алюминиевого сплава и строительной (малоуглеродистой) стали при увеличении их температуры на 50 ºС.
Для алюминиевого стержня (α = 23·10 6 , Е = 70000 Н/мм 2 ):
σ = 70000·23·10 -6 ·50 = 80,5 Н/мм 2
Для стержня из малоуглеродистой стали (α = 12·10 6 , Е = 210000 Н/мм 2 ):
σ = 210000·12·10 -6 ·50 = 126 Н/мм 2
Отметим известный факт, что при одинаковом изменении температуры температурные напряжения в алюминиевом стержне составляют только 2/3 от величины температурных напряжений в стальном стержне. Так происходит потому, что величина температурных напряжений зависит от произведения модуля упругости и коэффициента температурного расширения (см. формулу (3)). Поэтому, хотя коэффициент температурного расширения алюминия в два раза больше, чем у стали, но модуль упругости алюминия в три раза меньше, чем у стали.
Как видно из приведенных выше расчетов, температурные напряжения могут достигать величин, сравнимых с напряжениями от механических нагрузок. Поэтому термические воздействия на конструкции зданий необходимо учитывать наряду с другими нагрузками, как того и требуют нормативные документы [4, 5].
1.5. Температурные перемещения
Вернемся к бруску материала, показанного на рисунке 1 [1]. Предполагаем, что материал бруска является гомогенным и изотропным, то есть механические свойства материала бруска являются одинаковыми во всем его объеме. Кроме того, предполагаем, что изменение температуры ΔT является однородным, то есть одинаковым, по всему бруску. При таких условиях мы можем вычислить увеличение любого размера бруска путем умножения первоначального размера на температурную деформацию. Например, если один из размеров бруска составляет L, то этот размер увеличиться на величину
δТ = εT· L= α·ΔT·L (4)
Уравнение (4) можно применять для вычисления изменений длин элементов конструкций после однородного нагрева, например, удлинение призматического стержня на рисунке 2.2. Поперечные размеры стержня также изменятся, но эти изменения не показаны на рисунке 2.2, так как обычно они не оказывают влияния на осевые силы, которые передаются этим стержнем.

Рисунок 2.2 – Увеличение длины призматического стрежня
в результате однородного увеличения температуры (уравнение (4)) [1]
Оценим удлинение незакрепленных алюминиевого и стального стержней длиной 3 м при увеличении их температуры на 50 ºС.
Для алюминиевого стержня:
δТ = α·ΔT·L = 23·10 -6 ·50·3000 = 3,5 мм
Для стержня из малоуглеродистой стали:
δТ = α·ΔT·L = 12·10 -6 ·50·3000 = 1,8 мм
При рассмотрении выше температурных деформаций предполагалось, что конструкция не имеет ограничений для своих перемещений, что позволяло ей расширяться или сокращаться совершенно свободно. Такие условия возникают, например, когда объект лежит на гладкой поверхности, на которой не возникает трения [1]. В таких случаях при однородном нагреве всего объекта в целом не возникает напряжений, хотя неоднородные изменения температуры могут вызывать внутренние температурные напряжения. Однако многие конструкции имеют опоры, которые препятствуют свободному расширению и сокращению их размеров. Поэтому в них развиваются температурные напряжения даже, если изменение температуры является однородным по всей конструкции.
1.6. Температурные деформации в статически определимых конструкциях
Рассмотрим ферму АВС из двух стержней, показанную на рисунке 2.3. Предположим, что температура стержня АВ изменилась на ΔТ1, а стержня ВС – на ΔТ2. Поскольку эта ферма является статически определимой, то оба стержня могут свободно удлиняться или укорачиваться, давая в результате перемещение соединения В. Однако в этом случае температурные напряжения в стержнях, а также реакции в опорах, отсутствуют.

Рисунок 2.3 – Статически определимая ферма
с однородным изменением температуры в каждом элементе
Это заключение справедливо в целом для всех статически определимых конструкций, а именно: однородное изменение температуры в элементах конструкции вызывают температурные деформации (и соответствующие изменения длин элементов) без возникновения соответствующих температурных напряжений [1, 2].
1.7. Температурные деформации в статически неопределимых конструкциях
Статически неопределимыми конструкциями называются конструкции, у которых число реакций превышает число уравнений статического равновесия. В отличие от статически определимых конструкций при расчете таких конструкций принимаются во внимание прогибы [1, 2].
В статически неопределимой конструкции температурные напряжения могут возникать или не возникать в зависимости от особенностей конструкции и особенностей температурных изменений. Чтобы проиллюстрировать некоторые из таких возможностей, рассмотрим статически неопределимую ферму, показанную на рисунке 2.4.

Рисунок 2.4 — Статически неопределимая ферма
под воздействием изменений температуры
Опоры этой конструкции позволяют узлу D двигаться горизонтально. Поэтому, когда вся ферма однородно нагревается, в ней не возникает температурных напряжений. Все элементы увеличиваются в длине пропорционально своим первоначальным длинам, а вся ферма в целом становится немного больше в размерах.
Однако, если некоторые из стержней нагреваются, а другие – нет, то возникают температурные напряжения, так как статически неопределимое расположение стержней препятствует их свободному расширению.
Заключение
1) Изменение температуры элементов конструкции вызывает в них температурные деформации. Температурные напряжения возникают только в статически неопределимых конструкциях.
2) Однородный нагрев алюминиевого стержня на 50 ºС способен при жестком закреплении концов стержня вызывать значительные температурные напряжения. При таком нагреве удлинение стержня со свободными концами составляет 3,5 мм.
Источники:
1. James M. Gere & Barry J. Goodno — Mechanics of Materials, 2009
2. Тимошенко С.П., Гере Дж. – Механика материалов, М.: Мир, 1976
3. Aluminum and Aluminum Alloys / ed. J.R. Davis, ASM International, 1993
4. СП 128.13330.2012 (СНИП 2.03.06-85) Алюминиевые конструкции
5. EN 1991-1-5 Еврокод 1: Воздействия на сооружения. Часть 1-5. Основные воздействия. Температурные воздействия
ООО «Алюком»
г. Москва, ул. Нагатинская, д. 16, стр. 9, офис 2-5
Тел.: +7 (495) 268 0444
E-mail: info@alucom.ru
Москва, Рязанский проспект, д.8А, стр.17 (цех 17, территория завода ВНИИ МетМаш).
Заезд транспорта через КПП ул.Стахановская д.20.
Время работы:
Пн-Чт: 9:30-17:00,
Пт: 9:30-16:00.
- FAQ
- Вентилируемый фасад
- Фасадные системы Alucom
- Цена фасада
- Производство фасадов
- Алюминиевые фасады
Мы в социальных сетях:
Продвижение сайта — ADVcreative.ru
Ваше сообщение успешно отправлено
Ваше сообщение успешно отправлено
Ваше сообщение успешно отправлено
Как рассчитывают коэффициент линейного расширения бетона?
Для того чтобы построить прочное здание, специалисты определяют коэффициент линейного расширения бетона. Так строитель может узнать, на сколько изменится в длину материал после нагревания. Такие расчеты позволяют избежать преждевременной деформации постройки, появление трещин и увеличить эксплуатационную стойкость сооружения.
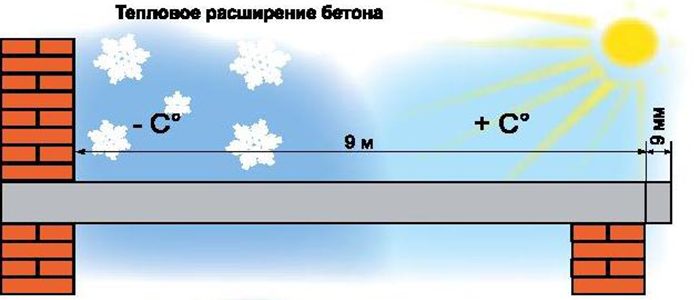
Что это такое?
Термин коэффициент расширения бетона обозначает, как сильно расширяется строительный материал при увеличении температуры.
Понятие связано с теплоемкостью и теплопроводностью раствора. Бетон, который может расширяться, имеет в составе добавки или напрягающий цемент. Таким образом, в результате получается стойкая смесь, которая способна изменяться в размере. Кроме этого, для создания конструкции необходимы швы, поддерживающие блоки. Если возникает слишком большой температурный перепад, то бетон может потрескаться. Для этого стараются правильно подобрать состав материала с высоким коэффициентом, поэтому можно предотвратить появление трещин.
Как рассчитать показатель температурного расширения?
Можно самостоятельно измерить расширение. Для этого измеряется исходная длина. После температура повышается на 1 градус. Стоит помнить, что уровень тепла должен быть одинаковый по всему периметру. После уточняют величину удлинения. Для микроизменений используют микроскоп. Кроме этого, коэффициент теплового расширения бетона можно вычислить по формуле: l=l0(1+α⋅ΔT). В этом уравнении l обозначает расширение, ΔT — температуру, при которой произошли изменения, а l0 — начальная длина.
Температурный показатель
Коэффициент можно найти в таблице, в которой даются средние значения. По табличным данным для бетона этот показатель равен 0,00001 (ºС)-1. Так, при 80 градусах увеличение будет 0,8 мм/м. Но такие табличные данные не являются довольно точными, так как во всех схемах предоставлены усредненные значения. Потому желательно самостоятельно измерять или рассчитывать показатели.

Теплоемкость
Коэффициент температурного расширения неразрывно связан с теплоемкостью, используемых при строительстве. Под этим термином подразумевает определенное количество тепла, которое нужно смеси для того, чтобы поднять температуру. Так как выделяют несколько типов растворов, то и коэффициент будет меняться от наполнителей. Так, теплоемкость воздушно-сухого бетона равняется 1,35 Вт (м*°С). Это говорит о том, что показатель высокий и потому нужен дополнительный утеплитель. У пористых смесей значение теплоемкости низкое (0,35—0,75 ВТ).
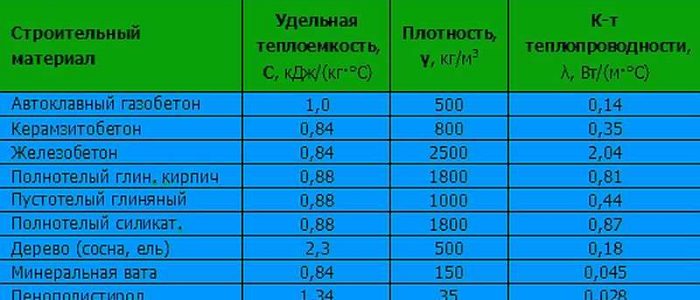
Как регулировать?
Значение зависит от таких факторов:
- температуры;
- класс;
- наполнителя.
Заполнитель и цемент имеют разный температурный коэффициент. Потому при нагревании и расширении может происходить деформация и появляются трещины. Для того чтобы это не произошло применяют специальные швы. Кроме этого, увеличивают армирование строительной конструкции. Бетон делят на отдельные блоки. Но эти методы дорогостоящие и не всегда эффективны. Потому для результата используют напрягающие и расширяющие вяжущие.
Температурный коэффициент линейного расширения металлов, твердых веществ, жидкостей (Таблица)

Термин коэффициент расширения бетона обозначает, как сильно расширяется строительный материал при увеличении температуры.
Понятие связано с теплоемкостью и теплопроводностью раствора. Бетон, который может расширяться, имеет в составе добавки или напрягающий цемент. Таким образом, в результате получается стойкая смесь, которая способна изменяться в размере. Кроме этого, для создания конструкции необходимы швы, поддерживающие блоки. Если возникает слишком большой температурный перепад, то бетон может потрескаться. Для этого стараются правильно подобрать состав материала с высоким коэффициентом, поэтому можно предотвратить появление трещин.
1.7. Температурные деформации в статически неопределимых конструкциях
Статически неопределимыми конструкциями называются конструкции, у которых число реакций превышает число уравнений статического равновесия. В отличие от статически определимых конструкций при расчете таких конструкций принимаются во внимание прогибы [1, 2].
В статически неопределимой конструкции температурные напряжения могут возникать или не возникать в зависимости от особенностей конструкции и особенностей температурных изменений. Чтобы проиллюстрировать некоторые из таких возможностей, рассмотрим статически неопределимую ферму, показанную на рисунке 2.4.
Рисунок 2.4 — Статически неопределимая ферма под воздействием изменений температуры
Читайте также: Сколько мешков цемента необходимо на 1 куб бетона
Опоры этой конструкции позволяют узлу D двигаться горизонтально. Поэтому, когда вся ферма однородно нагревается, в ней не возникает температурных напряжений. Все элементы увеличиваются в длине пропорционально своим первоначальным длинам, а вся ферма в целом становится немного больше в размерах.
Однако, если некоторые из стержней нагреваются, а другие – нет, то возникают температурные напряжения, так как статически неопределимое расположение стержней препятствует их свободному расширению.
Как рассчитать показатель температурного расширения?

Чтобы определить данный показатель, нужно сделать замер длины изделия до повышенного термического воздействия.
Можно самостоятельно измерить расширение. Для этого измеряется исходная длина. После температура повышается на 1 градус. Стоит помнить, что уровень тепла должен быть одинаковый по всему периметру. После уточняют величину удлинения. Для микроизменений используют микроскоп. Кроме этого, коэффициент теплового расширения бетона можно вычислить по формуле: l=l0(1+α⋅ΔT). В этом уравнении l обозначает расширение, ΔT — температуру, при которой произошли изменения, а l0 — начальная длина.
Температурно усадочные швы
Температурно усадочные швы, в России должны быть начиная от 1.1 мм на 1м, делая вывод из расчета 0.3 мм — это усадка + 0.8 — температурный коэффициент. В строительных нормах и правилах (СНИП), размеры больше, так же стоит учитывать и то, что изменения температур порядка 80 ºС и больше, вызывают трещины в бетоне, который имеет жесткий наполнитель внутри, потому что существует разница коэффициентов расширения раствора и внутреннего наполнителя.
- Дома из пенобетонных блоков
- Сколько цемента в кубе бетона
Температурный показатель
Коэффициент можно найти в таблице, в которой даются средние значения. По табличным данным для бетона этот показатель равен 0,00001 (ºС)-1. Так, при 80 градусах увеличение будет 0,8 мм/м. Но такие табличные данные не являются довольно точными, так как во всех схемах предоставлены усредненные значения. Потому желательно самостоятельно измерять или рассчитывать показатели.

Данный показатель для каждого вида материала будет отличаться.
Температурный коэффициент линейного расширения
| Материал | Коэффициент линейного теплового расширения | |
| 10-6 °С-1 | 10-6 °F-1 | |
| ABS (акрилонитрил-бутадиен-стирол) термопласт | 73.8 | 41 |
| ABS — стекло, армированное волокнами | 30.4 | 17 |
| Акриловый материал, прессованный | 234 | 130 |
| Алмаз | 1.1 | 0.6 |
| Алмаз технический | 1.2 | 0.67 |
| Алюминий | 22.2 | 12.3 |
| Ацеталь | 106.5 | 59.2 |
| Ацеталь , армированный стекловолокном | 39.4 | 22 |
| Ацетат целлюлозы (CA) | 130 | 72.2 |
| Ацетат бутират целлюлозы (CAB) | 25.2 | 14 |
| Барий | 20.6 | 11.4 |
| Бериллий | 11.5 | 6.4 |
| Бериллиево-медный сплав (Cu 75, Be 25) | 16.7 | 9.3 |
| Бетон | 14.5 | 8.0 |
| Бетонные структуры | 9.8 | 5.5 |
| Бронза | 18.0 | 10.0 |
| Ванадий | 8 | 4.5 |
| Висмут | 13 | 7.3 |
| Вольфрам | 4.3 | 2.4 |
| Гадолиний | 9 | 5 |
| Гафний | 5.9 | 3.3 |
| Германий | 6.1 | 3.4 |
| Гольмий | 11.2 | 6.2 |
| Гранит | 7.9 | 4.4 |
| Графит, чистый | 7.9 | 4.4 |
| Диспрозий | 9.9 | 5.5 |
| Древесина, пихта, ель | 3.7 | 2.1 |
| Древесина дуба, параллельно волокнам | 4.9 | 2.7 |
| Древесина дуба , перпендикулярно волокнам | 5.4 | 3.0 |
| Древесина, сосна | 5 | 2.8 |
| Европий | 35 | 19.4 |
| Железо, чистое | 12.0 | 6.7 |
| Железо, литое | 10.4 | 5.9 |
| Железо, кованое | 11.3 | 6.3 |
| Золото | 14.2 | 8.2 |
| Известняк | 8 | 4.4 |
| Инвар (сплав железа с никелем) | 1.5 | 0.8 |
| Инконель (сплав) | 12.6 | 7.0 |
| Иридий | 6.4 | 3.6 |
| Иттербий | 26.3 | 14.6 |
| Иттрий | 10.6 | 5.9 |
| Кадмий | 30 | 16.8 |
| Калий | 83 | 46.1 — 46.4 |
| Кальций | 22.3 | 12.4 |
| Каменная кладка | 4.7 — 9.0 | 2.6 — 5.0 |
| Каучук, твердый | 77 | 42.8 |
| Кварц | 0.77 — 1.4 | 0.43 — 0.79 |
| Керамическая плитка (черепица) | 5.9 | 3.3 |
| Кирпич | 5.5 | 3.1 |
| Кобальт | 12 | 6.7 |
| Констанан (сплав) | 18.8 | 10.4 |
| Корунд, спеченный | 6.5 | 3.6 |
| Кремний | 5.1 | 2.8 |
| Лантан | 12.1 | 6.7 |
| Латунь | 18.7 | 10.4 |
| Лед | 51 | 28.3 |
| Литий | 46 | 25.6 |
| Литая стальная решетка | 10.8 | 6.0 |
| Лютеций | 9.9 | 5.5 |
| Литой лист из акрилового пластика | 81 | 45 |
| Магний | 25 | 14 |
| Марганец | 22 | 12.3 |
| Медноникелевый сплав 30% | 16.2 | 9 |
| Медь | 16.6 | 9.3 |
| Молибден | 5 | 2.8 |
| Монель-металл (никелево-медный сплав) | 13.5 | 7.5 |
| Мрамор | 5.5 — 14.1 | 3.1 — 7.9 |
| Мыльный камень (стеатит) | 8.5 | 4.7 |
| Мышьяк | 4.7 | 2.6 |
| Натрий | 70 | 39.1 |
| Нейлон, универсальный | 72 | 40 |
| Нейлон, Тип 11 (Type 11) | 100 | 55.6 |
| Нейлон, Тип 12 (Type 12) | 80.5 | 44.7 |
| Нейлон литой , Тип 6 (Type 6) | 85 | 47.2 |
| Нейлон, Тип 6/6 (Type 6/6), формовочный состав | 80 | 44.4 |
| Неодим | 9.6 | 5.3 |
| Никель | 13.0 | 7.2 |
| Ниобий (Columbium) | 7 | 3.9 |
| Нитрат целлюлозы (CN) | 100 | 55.6 |
| Окись алюминия | 5.4 | 3.0 |
| Олово | 23.4 | 13.0 |
| Осмий | 5 | 2.8 |
| Палладий | 11.8 | 6.6 |
| Песчаник | 11.6 | 6.5 |
| Платина | 9.0 | 5.0 |
| Плутоний | 54 | 30.2 |
| Полиалломер | 91.5 | 50.8 |
| Полиамид (PA) | 110 | 61.1 |
| Поливинилхлорид (PVC) | 50.4 | 28 |
| Поливинилденфторид (PVDF) | 127.8 | 71 |
| Поликарбонат (PC) | 70.2 | 39 |
| Поликарбонат — армированный стекловолокном | 21.5 | 12 |
| Полипропилен — армированный стекловолокном | 32 | 18 |
| Полистирол (PS) | 70 | 38.9 |
| Полисульфон (PSO) | 55.8 | 31 |
| Полиуретан (PUR), жесткий | 57.6 | 32 |
| Полифенилен — армированный стекловолокном | 35.8 | 20 |
| Полифенилен (PP), ненасыщенный | 90.5 | 50.3 |
| Полиэстер | 123.5 | 69 |
| Полиэстер, армированный стекловолокном | 25 | 14 |
| Полиэтилен (PE) | 200 | 111 |
| Полиэтилен — терефталий (PET) | 59.4 | 33 |
| Празеодимий | 6.7 | 3.7 |
| Припой 50 — 50 | 24.0 | 13.4 |
| Прометий | 11 | 6.1 |
| Рений | 6.7 | 3.7 |
| Родий | 8 | 4.5 |
| Рутений | 9.1 | 5.1 |
| Самарий | 12.7 | 7.1 |
| Свинец | 28.0 | 15.1 |
| Свинцово-оловянный сплав | 11.6 | 6.5 |
| Селен | 3.8 | 2.1 |
| Серебро | 19.5 | 10.7 |
| Скандий | 10.2 | 5.7 |
| Слюда | 3 | 1.7 |
| Сплав твердый (Hard alloy) K20 | 6 | 3.3 |
| Сплав хастелой (Hastelloy) C | 11.3 | 6.3 |
| Сталь | 13.0 | 7.3 |
| Сталь нержавеющая аустенитная (304) | 17.3 | 9.6 |
| Сталь нержавеющая аустенитная (310) | 14.4 | 8.0 |
| Сталь нержавеющая аустенитная (316) | 16.0 | 8.9 |
| Сталь нержавеющая ферритная (410) | 9.9 | 5.5 |
| Стекло витринное (зеркальное, листовое) | 9.0 | 5.0 |
| Стекло пирекс, пирекс | 4.0 | 2.2 |
| Стекло тугоплавкое | 5.9 | 3.3 |
| Строительный (известковый) раствор | 7.3 — 13.5 | 4.1-7.5 |
| Стронций | 22.5 | 12.5 |
| Сурьма | 10.4 | 5.8 |
| Таллий | 29.9 | 16.6 |
| Тантал | 6.5 | 3.6 |
| Теллур | 36.9 | 20.5 |
| Тербий | 10.3 | 5.7 |
| Титан | 8.6 | 4.8 |
| Торий | 12 | 6.7 |
| Тулий | 13.3 | 7.4 |
| Уран | 13.9 | 7.7 |
| Фарфор | 3.6-4.5 | 2.0-2.5 |
| Фенольно-альдегидный полимер без добавок | 80 | 44.4 |
| Фторэтилен пропилен (FEP) | 135 | 75 |
| Хлорированный поливинилхлорид (CPVC) | 66.6 | 37 |
| Хром | 6.2 | 3.4 |
| Цемент | 10.0 | 6.0 |
| Церий | 5.2 | 2.9 |
| Цинк | 29.7 | 16.5 |
| Цирконий | 5.7 | 3.2 |
| Шифер | 10.4 | 5.8 |
| Штукатурка | 16.4 | 9.2 |
| Эбонит | 76.6 | 42.8 |
| Эпоксидная смола , литая резина и незаполненные продукты из них | 55 | 31 |
| Эрбий | 12.2 | 6.8 |
| Этилен винилацетат (EVA) | 180 | 100 |
| Этилен и этилакрилат (EEA) | 205 | 113.9 |
| Эфир виниловый | 16 — 22 | 8.7 — 12 |
Примечание: источниками справочных данных являются публикации в Интернете, поэтому они не могут считаться «официальными» и «абсолютно точными». Как правило, в Интернет справочниках не приводятся ссылки на научные работы, являющиеся основой опубликованных данных. Мы стараемся брать информацию из наиболее надежных научных сайтов. Однако если кого-то интересуют ссылки на эксперименты, советуем произвести самостоятельно углубленный поиск в Интернете. Будем признательны за любые комментарии к нашим справочным таблицам, а особенно за уточнения существующей информации или дополнение справочных данных.
Вас также может заинтересовать:
Коэффициент объемного расширения
ТКЛР материалов, используемых в электронике
Теплоемкость
Коэффициент температурного расширения неразрывно связан с теплоемкостью, используемых при строительстве. Под этим термином подразумевает определенное количество тепла, которое нужно смеси для того, чтобы поднять температуру. Так как выделяют несколько типов растворов, то и коэффициент будет меняться от наполнителей. Так, теплоемкость воздушно-сухого бетона равняется 1,35 Вт (м*°С). Это говорит о том, что показатель высокий и потому нужен дополнительный утеплитель. У пористых смесей значение теплоемкости низкое (0,35—0,75 ВТ).

Данный коэффициент зависит и от теплоемкости материала.
Коэффициент термического расширения бетона
Читайте также: Что такое тощий бетон и в каких целях он используется
Величина коэффициента термического расширения бетона зависит от состава бетонной смеси и влажности в период изменения температуры. Цементный камень и заполнитель имеют разные коэффициенты термического расширения, а коэффициент термического расширения бетона отражает соотношение материалов в составе бетона.
Коэффициент термического расширения цементного камня колеблется в пределах от 10ХЮ6 до 18,ЗХЮ6 на 1°С. Он больше, чем у заполнителя. Коэффициент термического расширения бетона зависит от количества заполнителя в смеси (табл. 7.10) и коэффициента расширения заполнителя.
Влияние влажности обусловлено составляющими цементного камня и определяется тем, что коэффициент термического расширения слагается из двух частей: действительного кинетического термического коэффициента и давления набухания.
Последнее увеличивается с уменьшением капиллярного давления воды в цементном камне при повышении температуры. Набухание невозможно, если образец сухой, т.е. не содержит воды, и если он насыщен. Следовательно, при этих двух предельных состояниях коэффициент термического расширения меньше, чем при частичном насыщении.
На рис. 7.25 и 7.26 приведены данные для цементного камня. В бетоне мы наблюдаем те же зависимости, хотя коэффициент термического расширения меняется меньше, так как только цементный камень реагирует на изменение влажности и возраст. В табл. 7.11 приведены значения коэффициентов термического расширения бетона состава 1 :6, твердевшего на воздухе при 64%-ной относительной влажности, в воде и увлажненного после воздушного твердения.
Только величины, определенные на насыщенных и высушенных образцах, дают действительные значения коэффициента термического расширения, но величины при промежуточных значениях влажности необходимы, так как они отражают реальные условия эксплуатации бетона Ьсли повышение температуры при переходе от зимы к лету сопровождается высыханием, появляется усадка и чистое расширение меньше чем при отсутствии потери бетоном воды.
Химический состав и тонкость помола цемента влияют на величину коэффициента термического расширения лишь постольку, поскольку они влияют на свойства в раннем возрасте. Наличие воздушных пор влияния не оказывает.
Все сказанное относится к нормальным температурам ниже 40° С.
Более высокие температуры могут встречаться, например, в аэродромных покрытиях при действии отходящих газов реактивных двигателей и в производственных условиях. На рис. 7.27 показано, что при температуре выше 320°С коэффициент термического расширения бетона возрастает, возможно, вследствие дегидратации цементного камня. Значения коэффициента термического расширения приведены в табл. 7.12.
Лабораторные испытания показали, что бетоны с большим коэффициентом термического расширения менее стойки к изменениям температуры, чем бетоны с меньшим значением коэффициента расширения. На рис. 7.28 показаны результаты испытаний бетона, подвергавшегося повторному нагреванию и охлаждению в интервале температур 4,4—60° С со скоростью 2,4° в минуту. Однако коэффициент термического расширения не может служить количественной характеристикой долговечности бетона, подвергающегося частым или быстрым изменениям температуры.
Но более быстрое изменение температуры, чем в обычных условиях, может вызвать разрушение бетона. На рис. 7.29 показано влияние быстрого охлаждения после нагревания до указанной температуры.
Как регулировать?
Значение зависит от таких факторов:
- температуры;
- класс;
- наполнителя.
Заполнитель и цемент имеют разный температурный коэффициент. Потому при нагревании и расширении может происходить деформация и появляются трещины. Для того чтобы это не произошло применяют специальные швы. Кроме этого, увеличивают армирование строительной конструкции. Бетон делят на отдельные блоки. Но эти методы дорогостоящие и не всегда эффективны. Потому для результата используют напрягающие и расширяющие вяжущие.
Усадочно-температурные деформации бетона
Источник https://alucom.ru/articles/zarubej_opit/temperaturnye_vozdejstviya_na_konstrukcii_chast_2_termomehanika
Источник https://znaybeton.ru/proizvodstvo/raschety/koeffitsient-temperaturnogo-rasshireniya-betona.html
Источник https://stroi-s-ka.ru/tehnologii/koefficient-rasshireniya-betona.html





